

Said differently, the entropy of $X$ is simply the average self-information over all of the possible outcomes of $X$.
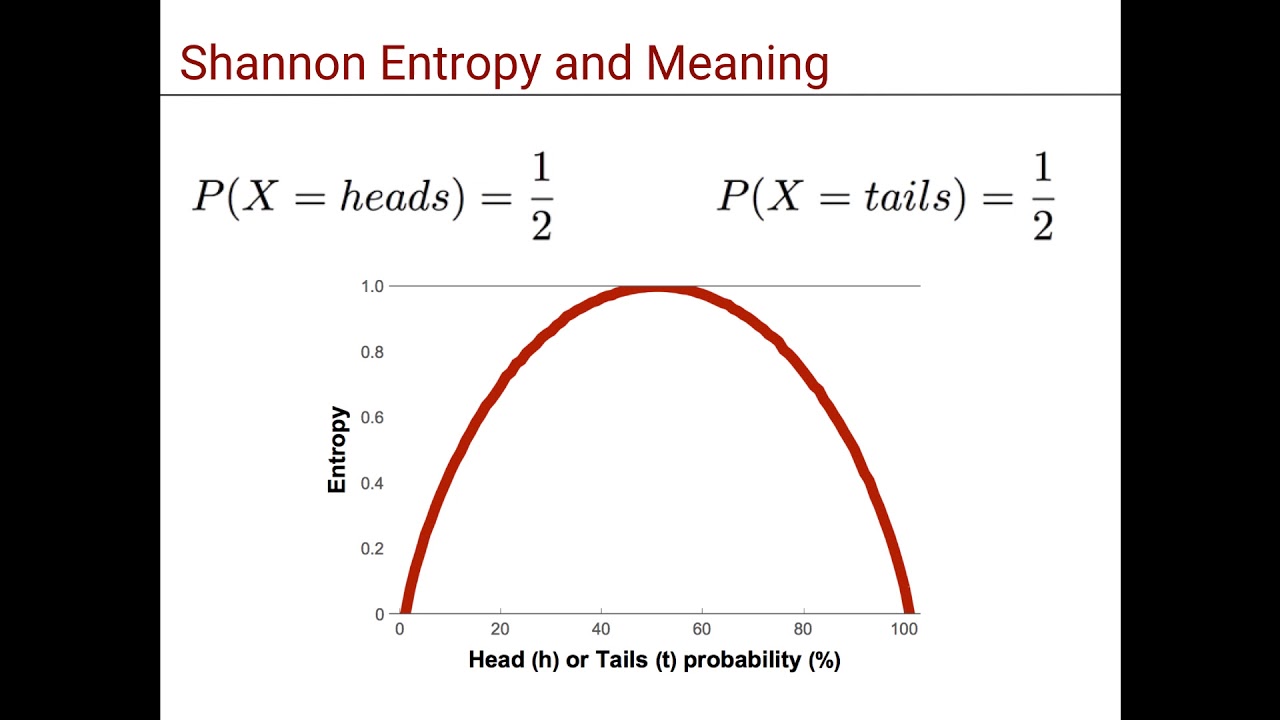
Given a random variable $X$, the entropy of $X$, denoted $H(X)$ is simply the expected self-information over its outcomes:\ = -\sum_$ is the codomain of $X$. The concept of information entropy extends this idea to discrete random variables. Given an event within a probability space, self-information describes the information content inherent in that event occuring. In turn, this discussion will explain how the base of the logarithm used in $I$ corresponds to the number of symbols that we are using in a hypothetical scenario in which we wish to communicate random events.
It is within this context that the concept of information entropy begins to materialize. Why is that? In this post, we will place the idea of “information as surprise” within a context that involves communicating surprising events between two agents. One strange thing about this equation is that it seems to change with respect to the base of the logarithm. Thus, in information theory, information is a function, $I$, called self-information, that operates on probability values $p \in $:\ We discussed how surprise intuitively should correspond to probability in that an event with low probability elicits more surprise because it is unlikely to occur. In the first post of this series, we discussed how Shannon’s Information Theory defines the information content of an event as the degree of surprise that an agent experiences when the event occurs. In this second post, we will build on this foundation to discuss the concept of information entropy. In the first post, we discussed the concept of self-information.
#Information entropy series
In this series of posts, I will attempt to describe my understanding of how, both philosophically and mathematically, information theory defines the polymorphic, and often amorphous, concept of information. The mathematical field of information theory attempts to mathematically describe the concept of “information”. If there is a 100-0 probability that a result will occur, the entropy is 0.Information entropy (Foundations of information theory: Part 2) It does not involve information gain because it does not incline towards a specific result more than the other. In the context of a coin flip, with a 50-50 probability, the entropy is the highest value of 1. The information gain is a measure of the probability with which a certain result is expected to happen. It has applications in many areas, including lossless data compression, statistical inference, cryptography, and sometimes in other disciplines as biology, physics or machine learning. The "average ambiguity" or Hy(x) meaning uncertainty or entropy. It measures the average ambiguity of the received signal." "The conditional entropy Hy(x) will, for convenience, be called the equivocation. Information and its relationship to entropy can be modeled by: R = H(x) - Hy(x) The concept of information entropy was created by mathematician Claude Shannon. More clearly stated, information is an increase in uncertainty or entropy. In general, the more certain or deterministic the event is, the less information it will contain. It tells how much information there is in an event. Information entropy is a concept from information theory.


 0 kommentar(er)
0 kommentar(er)
